The NEW BATPAKS Are Here!
The NEW BATPAKS Are Here!
Add description, images, menus and links to your mega menu
A column with no settings can be used as a spacer
Link to your collections, sales and even external links
Add up to five columns
Add description, images, menus and links to your mega menu
A column with no settings can be used as a spacer
Link to your collections, sales and even external links
Add up to five columns
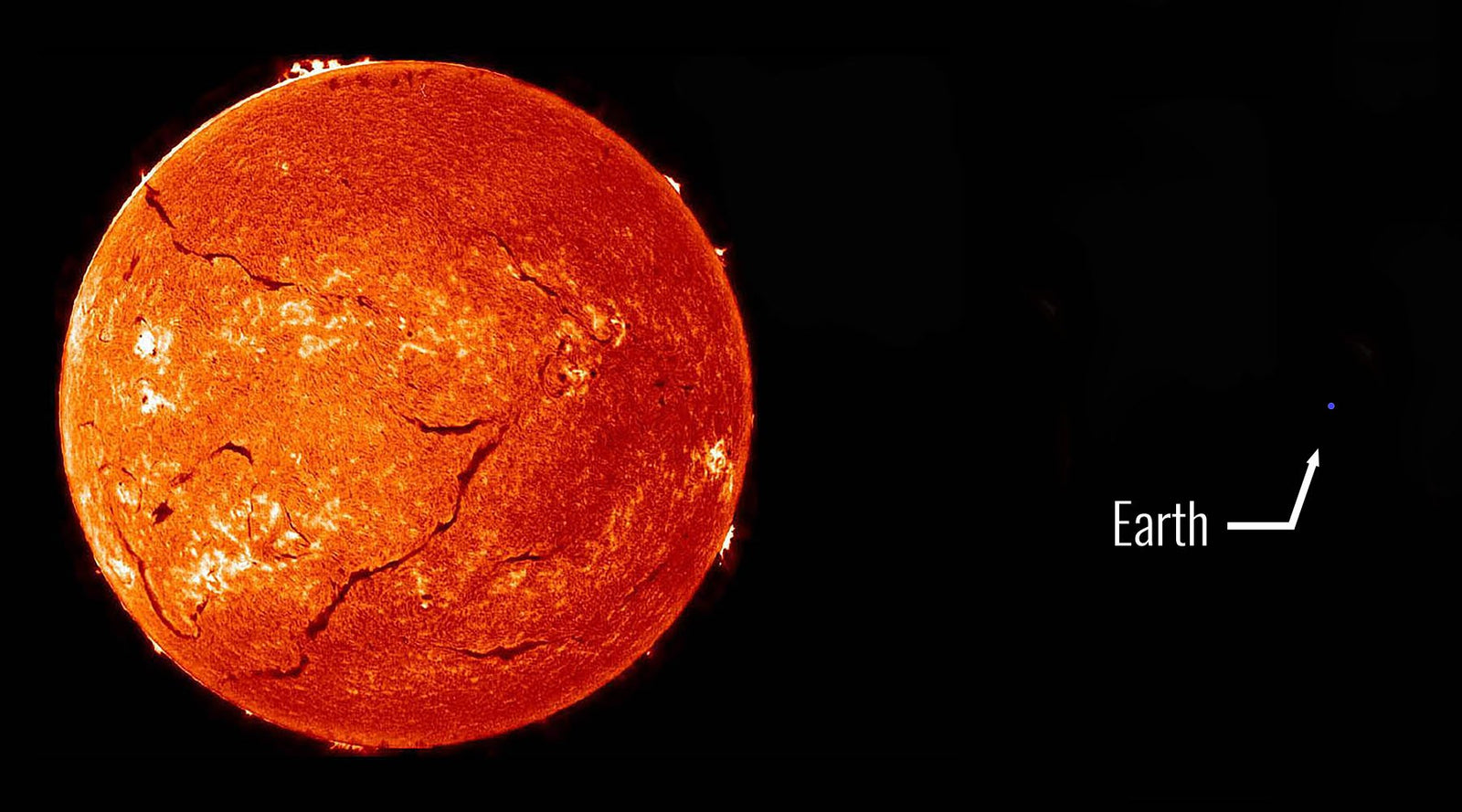
How Many Lumens is the Sun?
May 17, 2019 3 min read
How Many Lumens is the Sun?
When people ask the question, "How many Lumens is the Sun?", more often than not, there is another question they are really trying to answer. The underlying question may just be out of general curiosity, but usually we are trying to build some sort of intuitive understanding of how much light a lumen represents. We are bombarded with specifications for headlamps, flashlights, indoor lighting, outdoor lighting, LED lights, grow lights, incandescent, fluorescent, halogen, and the list goes on and on. We all have lots of experience with the sun and how bright it is under a variety of different circumstances. We are trying to relate our experiences to all these marketing specifications. It can be very confusing.
I'll try to clarify a number of these underlying questions by reformulating the original question a number of different ways and then provide answers to these new, and hopefully more helpful questions.
How Many Lumens Does the Sun Produce?
Another way to ask this, and the question we'll answer first is, "What is the total amount of visible light that is produced by the sun?" A lumen is a specific quantity of visible light. The sun produces a broad spectrum of electromagnetic energy. All the way from radio, microwave, infrared, visible, ultraviolet, x-ray, gamma, and cosmic rays. But the quantity of the lumen is only concerned with the narrow band of visible light.

Using data derived from ground-based solar telescopes, space shuttle missions, satellites, sounding rockets, high-altitude aircraft, and computer models, scientists and engineers in the space and solar energy communities have standardized on a value for average spectral irradiance for earth. This quantity, also known as the solar constant, is 1366.1 watts per square meter. Simply put, this is how bright the sun is at the distance of earths orbit. Another way to think about it is if you had a one meter by one meter solar panel riding on a satellite and it was oriented perpendicular to the sun's rays and 100% efficient across the entire electromagnetic spectrum, it would produce 1,366 watts of electricity. That's right around enough electricity to power a good blow dryer.

However, this is for the full spectrum of the sun. Since we are only concerned with visible light, we need to adjust this number to account for only what the eye is sensitive to. The way to do that is to either solve the above integral, or you can just take my word for it. For our sun or any star with a black body temperature of 5778 K, the answer is 93. For every watt our sun puts out, it produces 93 lumens of visible light. So at earth's orbit, for each square meter, our sun puts out 127,000 lumens. That is very bright. No wonder it hurts to stare at the sun. Better get some stylish sunglasses and put on that sunscreen just in case.

Now let's find the area of the sphere that has a radius corresponding to the earths distance from the sun. So with the radius equal to 92.96 million miles, one astronomical unit, or 149.6 billion meters, the area is 281,229,000,000,000,000,000,000 or 281.2 sextillion square meters. Now we just multiply that with 127,000 lumens per square meter and we get the grand total of 35,730,000,000,000,000,000,000,000,000 lumens.
Our sun puts out 35.73 octillion lumens. That's a lot of sunlight and just a little bit brighter than the brightest headlamp. I definitely don't want to be the one buying batteries for it. Maybe we could use rechargeable lithium ion batteries... Solar rechargeable!
How Many Lumens of Sunlight Hit the Earth?
The size of the sun and the earth in the picture at the top of this article are to scale. However, the distance between them is highly compressed. Even so, it is apparent that the vast majority of sunlight does not hit the earth. It can be calculated by taking the ratio of the surface areas of a 1 AU radius sphere and a circle with the radius of the earth. These quantities are 281.2 sextillion square meters and 127.8 trillion square meters respectively. This ratio tells us that there is 2.2 billion times more light that doesn't hit the earth than does. Using this ratio we can calculate that there are 16.24 quintillion lumens of sunlight that hit the earth.
Subscribe
Sign up to get the latest on sales, new releases and more …
